publications

2022

1. 

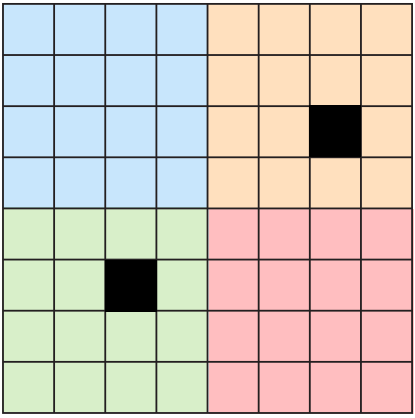   How deep convolutional neural networks lose spatial information with training

   Umberto M Tomasini *, Leonardo Petrini *, Francesco Cagnetta, and 1 more author

   arXiv preprint arXiv:2210.01506 2022

   Abs arXiv

   A central question of machine learning is how deep nets manage to learn tasks in high dimensions. An appealing hypothesis is that they achieve this feat by building a representation of the data where information irrelevant to the task is lost. For image datasets, this view is supported by the observation that after (and not before) training, the neural representation becomes less and less sensitive to diffeomorphisms acting on images as the signal propagates through the net. This loss of sensitivity correlates with performance, and surprisingly correlates with a gain of sensitivity to white noise acquired during training. These facts are unexplained, and as we demonstrate still hold when white noise is added to the images of the training set. Here, we (i) show empirically for various architectures that stability to image diffeomorphisms is achieved by both spatial and channel pooling, (ii) introduce a model scale-detection task which reproduces our empirical observations on spatial pooling and (iii) compute analitically how the sensitivity to diffeomorphisms and noise scales with depth due to spatial pooling. The scalings are found to depend on the presence of strides in the net architecture. We find that the increased sensitivity to noise is due to the perturbing noise piling up during pooling, after being rectified by ReLU units.

2. 

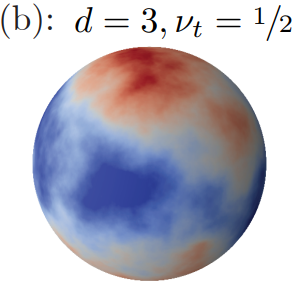   Learning sparse features can lead to overfitting in neural networks

   Leonardo Petrini *, Francesco Cagnetta *, Eric Vanden-Eijnden, and 1 more author

   Advances in Neural Information Processing Systems 2022

   Abs arXiv Poster

   It is widely believed that the success of deep networks lies in their ability to learn a meaningful representation of the features of the data. Yet, understanding when and how this feature learning improves performance remains a challenge: for example, it is beneficial for modern architectures trained to classify images, whereas it is detrimental for fully-connected networks trained on the same data. Here we propose an explanation for this puzzle, by showing that feature learning can perform worse than lazy training (via random feature kernel or the NTK) as the former can lead to a sparser neural representation. Although sparsity is known to be essential for learning anisotropic data, it is detrimental when the target function is constant or smooth along certain directions of input space. We illustrate this phenomenon in two settings: (i) regression of Gaussian random functions on the d-dimensional unit sphere and (ii) classification of benchmark datasets of images. For (i), we compute the scaling of the generalization error with the number of training points and show that methods that do not learn features generalize better, even when the dimension of the input space is large. For (ii), we show empirically that learning features can indeed lead to sparse and thereby less smooth representations of the image predictors. This fact is plausibly responsible for deteriorating the performance, which is known to be correlated with smoothness along diffeomorphisms.

2021

1. 

   Relative stability toward diffeomorphisms indicates performance in deep nets

   Leonardo Petrini, Alessandro Favero, Mario Geiger, and 1 more author

   Advances in Neural Information Processing Systems 2021

   Abs arXiv Poster

   Understanding why deep nets can classify data in large dimensions remains a challenge. It has been proposed that they do so by becoming stable to diffeomorphisms, yet existing empirical measurements support that it is often not the case. We revisit this question by defining a maximum-entropy distribution on diffeomorphisms, that allows studying typical diffeomorphisms of a given norm. We confirm that stability toward diffeomorphisms does not strongly correlate to performance on benchmark data sets of images. By contrast, we find that the stability toward diffeomorphisms relative to that of generic transformations R_f correlates remarkably with the test error \epsilon_t. It is of order unity at initialization but decreases by several decades during training for state-of-the-art architectures. For CIFAR10 and 15 known architectures, we find \epsilon_t≈0.2\sqrtR_f, suggesting that obtaining a small R_f is important to achieve good performance. We study how R_f depends on the size of the training set and compare it to a simple model of invariant learning.

2. 

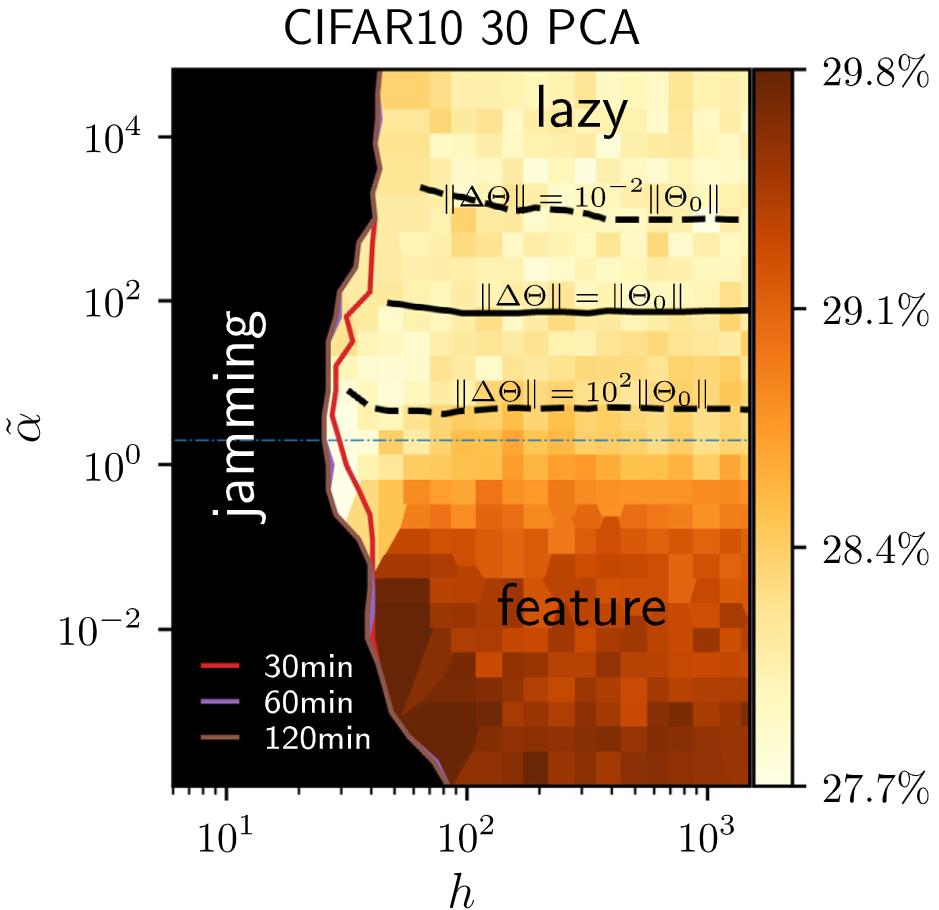   Landscape and training regimes in deep learning

   Mario Geiger, Leonardo Petrini, and Matthieu Wyart

   Physics Reports 2021

   Abs HTML

   Deep learning algorithms are responsible for a technological revolution in a variety of tasks including image recognition or Go playing. Yet, why they work is not understood. Ultimately, they manage to classify data lying in high dimension – a feat generically impossible due to the geometry of high dimensional space and the associated curse of dimensionality. Understanding what kind of structure, symmetry or invariance makes data such as images learnable is a fundamental challenge. Other puzzles include that (i) learning corresponds to minimizing a loss in high dimension, which is in general not convex and could well get stuck bad minima. (ii) Deep learning predicting power increases with the number of fitting parameters, even in a regime where data are perfectly fitted. In this manuscript, we review recent results elucidating (i,ii) and the perspective they offer on the (still unexplained) curse of dimensionality paradox. We base our theoretical discussion on the (h,α) plane where h controls the number of parameters and αthe scale of the output of the network at initialization, and provide new systematic measures of performance in that plane for two common image classification datasets. We argue that different learning regimes can be organized into a phase diagram. A line of critical points sharply delimits an under-parametrized phase from an over-parametrized one. In over-parametrized nets, learning can operate in two regimes separated by a smooth cross-over. At large initialization, it corresponds to a kernel method, whereas for small initializations features can be learned, together with invariants in the data. We review the properties of these different phases, of the transition separating them, and some open questions. Our treatment emphasizes analogies with physical systems, scaling arguments, and the development of numerical observables to quantitatively test these results empirically. Practical implications are also discussed, including the benefit of averaging nets with distinct initial weights, or the choice of parameters (h,α) optimizing performance.

3. 

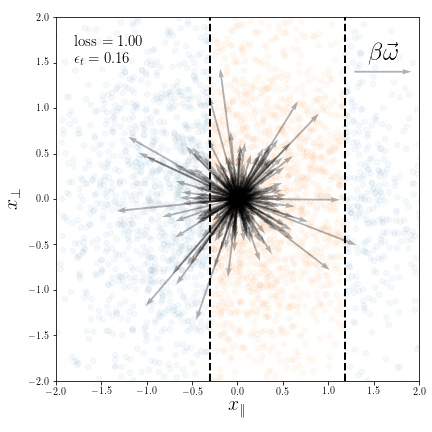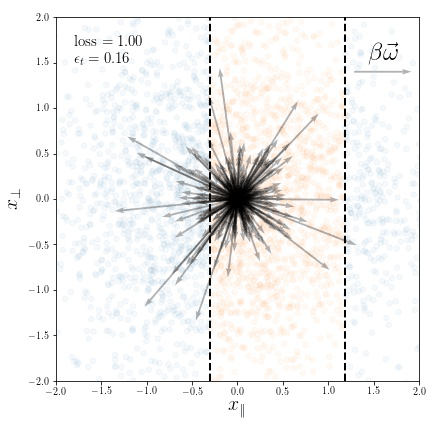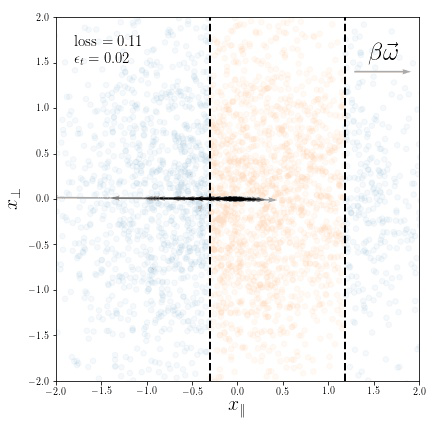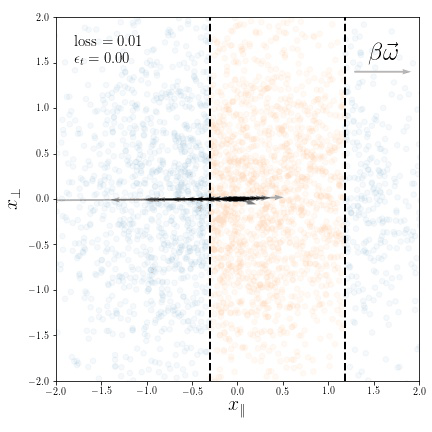   Geometric compression of invariant manifolds in neural networks

   Jonas Paccolat, Leonardo Petrini, Mario Geiger, and 2 more authors

   Journal of Statistical Mechanics: Theory and Experiment 2021

   arXiv